Introduction
The Важным направлением в вибрационной диагностики газотурбинных двигателей и газотурбинных двигателей авиационного газа является diagnostics с помощью моделирования. Моделирование дает возможность связать наличие некоторых видов дефектов машин с признаками его присутствия в сигнале вибрации. Одним из таких дефектов трещины появление в валах авиационных двигателей и газотурбинных двигателей, который составляет недопустимый. Таким образом, наиболее важная задача диагностической системы для обнаружения трещин во время и прогноз его развития.
Appearance трещины в результатах ротора в местном снижении жесткости. Величина потери жесткости зависит от геометрических характеристик трещины. Если статическая нагрузка, такие как силы тяжести применяются, трещина открывается и закрывается, когда ротор вращается. В результате, жесткость вала изменяется за цикл. Трещина в роторной системы приводит к Nfollowing изменений \\ в колебательном сигнале [1]:
· \\ п 1x гармоника скорости вращения из-за ростаincrease по амплитуде статического прогиба, вызванного уменьшением жесткости.
·appearance из 2х компонент скорости вращения за счет асимметричной жесткости ротора.
·appearance из 3х компонент скорости вращения из-за циклического открытия и закрытия трещины. \\ П \\ п \\ пThe основная задача математической модели является описанием стоимости и прав локального изменения жесткости в \\ п \\ п \\ пthe месте порог \\ п101; трещина имеет место, учитывая, как много факторов, как это возможно. \\ П \\ п \\ п
There несколько подходов к моделированию трещин. В простейших случаях трещины моделируются снижением радиальной жесткости всего вала [2,3,4]. В других случаях часть вала, порог \\ п101; трещина имеет место, это заме \\ п101, г эквивалентным элементом пучка. Коэффициенты матрицы жесткости такого элемента рассчитываются с учетом трещины и изменения в цикле. В работе [5] вычисление матрицы жесткости элемента балки с трещиной основано на использовании моментов инерции сечения балки с учетом трещины. В работе [6] матрица жесткости такого элемента вычисляется на основе уравнений механики разрушения твердых тел. Трещины можно моделировать упругой линии связи, соединяющей пограничные участки вала в месте его нахождения и давая трещины момент жесткость [7,8].
Change в трещины жесткости в зависимости от ее открытия и закрытия, когда ротор вращается, может быть описано математически разными способами. В простейшем случае можно предположить, что трещина имеет только две позиции: полностью&#
opened или полностью закрыт, а шаг функция может быть применена для описания его изменение жесткости математически [4]&\\ п. \\ п \\ п \\ п \\ п#work [3] описывает наиболее распространенные модели жесткости изменения. Одним из них является уравнение Gasch. Изменить&#\\ нин жесткость имеет место в зависимости от угла между фазой статической силы и фазой трещины и описываются 17 гармоник ряда Фурье. Та же статья дает Maes \\ п Davies уравнение WHER \\ п
101; жесткость изменяется в зависимости от угла в соответствии с косинус законом. В модели Ян жесткость изменяется по закону косинуса в степени относительной глубины трещины. \\ П \\ п \\ пЭта статье развивается модель трещины на основе existed подходов, а также представлена методика что дает возможность выделить признаки, используемых для определения его состояния для точного ротора.The алгоритм входит в программное обеспечение программы Динамика R4 [9], которая представляет собой выделенный
system на вычислении динамического поведения сложных роторных систем.
модельCrack&&#
Within принятая концепция моделирования, трещины в модели вала заменяются упругой линией, делящий вал на две части, и описывающий по жесткости матрицы с переменным коэффициенты. Если нет трещин, условие совместности деформаций между секциями частей вала осуществляется, так что все взаимные смещения запрещены. Введем вращающуюся систему координат ηOε, лежащих в области трещины, Рисунок 1. Его происхождение совпадает с началом координат неподвижной системы XYZ. Вал выполняет два движения - правильное вращение и прецессию вокруг оси Z.. При описании трещины мы рассмотрим только вращение вокруг п и е осей. Перемещения в других степеней свободы пренебрегают. \\ П \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ пFigure 1. Crack раздел \\ п \\ п \\ п \\ п \\ пFlexibility матрица линии имитации трещины во вращающейся системе координат, может быть записана как following:
\\ п
wher \\ п101;
Q \\ щ \\ на
\\ щ
вала угол поворота,\\ на
угол прецессии; \\ нг \\ урожденная(
Q) и
\\ нг \\ пHH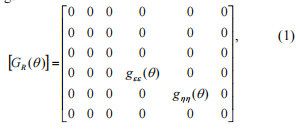
Q
\\ п) \\ п переменная coefficients гибкости моментов&#\\ п. =- Flexibility зависит от угла \\ п-Q \\ п because в то время как вал вращается, трещина открывается и закрывается. Жесткость матрица получается путем инверсии[ g-R ( Q)- ]matrix и нулевых коэффициентов гибкости при главная диагональ приводит к получению коэффициентов жесткости, уходящие в бесконечность. Мы предельное значение таких коэффициентов жесткости по 1е10 N \\ нм; это предположение не оказывает существенного влияния на результат, то есть, мы получаем \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п матрицыStiffness превращается в неподвижной системе координат, используя следующее уравнение: порога \\ п101; [\\ пT] \\ п матрица вращения (4), порога-101; \\ пС\\ п1COs (\\ п \\ щ
), \\ п \\ нСм\\ п1
sin (\\ п \\ щ )Умножение матриц в соответствии с уравнением (3), получаем:.\\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п Проведем некоторые преобразования, которые дают возможность перейти к более простому описанию трещины \\ п \\ пstiffness матрицы и алгоритм ее коэффициентов получение. В соответствии с моделью Maes, тоmay можно предположить, что радиальная гибкость кругового пучка с изменениями трещин от минимального до максимального значения по косинусу закона./
\\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п порога \\ п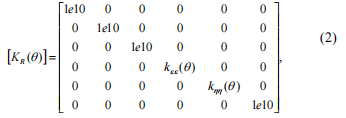
\\ п гибкость пучка с открытыми crack (максимальное значение). \\ П
we заменить трещины с помощью шарнира с моментом жесткости
\\ пк \\ пinit &#\\ нм \\ п \\ пк \\ п \\ п \\ п \\ п \\ п \\ п. Граничные условия пучка должны обеспечивать егоstatical определимость, как это показано на рисунке 2.-&#Figure 2 . Замена трещины с помощью шарнира=then радиальная гибкость выделенного участка вала с открытой трещины получается как:=\\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ пwher \\ п101;\\ пЕ\\ П модуль Юнга, \\ п
\\ п диаметральной момент инерции секции вала,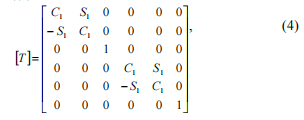
MH
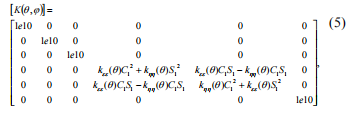
\\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п \\ п

Название работы: Product manager
отдел: Market Department
Телефон компании: +86 021-59150215
Электронная почта: Свяжитесь с нами
Мобильный телефон: +86 13817160919
Веб-сайт: lanzhusuperalloy.rub2b.com
Адрес: No. 2800 Caoxin Road, Xuhang Town, Jiading District, Shanghai