хуэр 101&#емодуль Юнга,-ярадиальный момент инерции осевого сечения,-K инициализацияMh - коэффициент жёсткости, соответствующий эквивалентному шарниру с полностью раскрытыми трещинами. в уравнении есть две суммирования - гибкость, связанная с трещинами, и гибкость без трещин.оно

 Следует отметить, что независимо от формы лонжерона, граничных условий и положения трещин, он вклад в гибкость лонжерона зависит только от коэффициента K инициализациямH ,Первое резюме. когда балка вращается, изменяется гибкость сечения трещины.У нас имеется следующая информация:хуэр 101 

 G О&#гибкость балки) без трещин  Q)=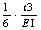 -KMhсуммарный аварийности тока жёсткости момента при заданной нагрузкеQ. -Интегрируйте два уравнения (5) и (7), и мы получим:хуэр101учитывая уравнение (6), мы получаем закон изменения жёсткости момента по фазе

 эйнштейний Q 

 :жёсткость момента эквивалентного шатуна зависит только от диаметра оси, свойств материала и глубины трещины.изменение положения трещины в ОСЕ, характеристики оси (включая опорное устройство) не изменят жёсткость момента эквивалентного шатуна (вверх)&#сечение с трещинами держится в том же состоянии, что и любое сечение трещиныПолучай.Возвращает ранее полученную матрицу жесткости, коэффициент жесткости которой может быть записан следующим образом: хуэр 

101 K

инициализация 

 Ee , K  инициализация 

 Угу. начальное значение жёсткости момента на соответствующей оси&#. задача Kинициализация Ee,Kинициализация  -Угу.расчеты могут быть разрешены двумя способами.Первое - вычисление жесткости изгибающего момента в программе с конечными элементами.Во - вторых, применять механику разрушения.Если известна геометрия, диаметр оси и свойства материала при разрезе отверстия, то есть возможность вычислить локальную гибкость открытой трещины [7,10].

 имитационный алгоритм системы ротора с трещинами следует получить коэффициент жесткости момента трещины через следующие шаги.создание в рамках специальной программы полной модели ротора для анализа динамики ротора (например:например, в динамических R4).выделить фрагменты ротора с трещинами.  трещины делят осевые сегменты на две подсистемы.ссылка, описанная матрицей переменныхкоэффициент жёсткости]к (q) 

 , 

J)]

заимствовать

размер 6x6 находится между подсистемами.

начальный коэффициент жёсткости момента

K

инициализация

Ee ,KинициализацияУгу.с помощью заданных методов можно получить открытое трещинное аналитическое решениесверху.Эти данные являются предварительными.при уравнении интегрального движения рассчитывается матричный коэффициент жёсткости смоделированного шатуна трещины 

Каждая роторная системаQ.матричное уравнение состояния нелинейной моделисистема ротора имеет следующую структуру: хуэр101]м ]

- матрица коэффициентов инерции;

 ] C ]

- матрица демпфирования и коэффициентов гироскопа;]к

] 

 матрица коэффициент жёсткости; {a&#U],{aU],{aU]- столбцы вибрационных ускорений, скорости вибрации и перемещений;{a-F(T)]&&любой тип динамической нагрузки - внутренняя и внешняя.матрица жесткости эквивалентного шатуна можно разделить на две части: константы и переменные, как показано ниже:]&к C] содержится в общей матрице жесткости конструкции]к]система.матрица() [q j] n,кдля вычисленияреакция на нелинейные ссылки:-хуэр101 

 U прием , 

 U гром– мусечение вращается вокруг соответствующей оси.окончательное уравнение движения системы показано ниже:Указанное уравнение можно решить с помощью числового метода (например, метод дракона)метод Кута, метод ньюмарка и т.д.сравнение гибкости обоих алгоритмов свидетельствует о достаточности алгоритмабалка - упортрещина, полученная при анализе конечных элементовоптимизация системы ячеек в соответствии с гипотетическим алгоритмом в динамическом R4.задача данной статьи - вычислить прогиб сечения трещины при воздействии удельной силы на различные стадии трещин и напряжений.На рисунке 3 показаны результаты проверки рекомендуемого алгоритма.были сопоставлены три результата:использовать метод конечных элементов (FEM) для расчета степени гибкости.В конечном элементе рассчитывается радиальная гибкость модели с разрезанными балками

Вся система углового положения трещины;&#Использовать динамический R4 для вычисления степени гибкости, использовать FEM для получения исходных данных.начальное значение моментажесткость трещины полного раскрытияK инициализацияEe, Kинициализация

Угу.получить по уравнению решения

K-инициализация

Mh-, а также радиальная гибкость трещинных балк

Gc-в соответствующем направлении вычисление производится методом конечных элементов.по закону (10) крепость момента на месте трещины в промежуточном углу от минимума до максимума;

используйте динамический R4 для вычисления мягкости.начальные данные о гибкости изгибающего момента при полном раскрытии трещин

-K-Ee

 инициализация , K-Угу.  

инициализацияалгоритм, используемый в механике разрушения, получен в аналитической форме [7,10].значение гибкости моментаПоложение трещины в промежуточном углу изменяется в соответствии с законом (10) от минимума до максимума.рис. 3 Изменение мягкости лонжерона в сечении трещины в каждом вращающемся кольце конечный результатмодель и динамика R4 очень близки к модели.разница между результатами вычислений и конечными результатами при начальных условиях составляет менее 1%.В то же время, первоначальный ориентировочный жесткости гораздо быстрее, чем расчет конечного элемента, и меньше времени, требуемого для работы, поэтому легче осуществитьдоходитьИспользуй.  геометрия и параметры ротора с трещинами Выберите геометрическую схему ротора с трещинами, чтобы показать оптимальное преимущество работы алгоритма, как показано в таблице 1ротор с центральным диском, кронштейн на конце оси.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②